Unit 2 ap calc ab practice – Welcome to the realm of Unit 2 AP Calculus AB Practice, where we embark on an exciting journey into the fascinating world of functions, limits, derivatives, and integrals. This comprehensive guide is meticulously crafted to provide a clear and engaging exploration of these fundamental concepts, empowering you to conquer the complexities of calculus with confidence.
Throughout this exploration, we will unravel the intricate nature of functions, their properties, and their diverse applications. We will delve into the concept of limits, exploring the various methods for finding them and their significance in calculus. Derivatives, the cornerstone of calculus, will be thoroughly examined, including their definitions, techniques for finding them, and their wide-ranging applications.
Unit 2 AP Calculus AB Practice: Functions
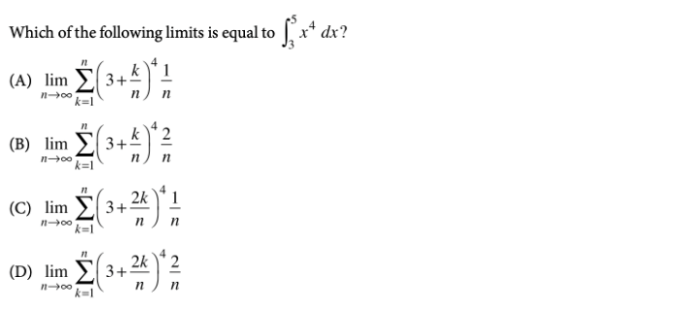
Functions are a fundamental concept in mathematics, representing a relationship between an input and an output. They are widely used in various fields, including science, engineering, and economics.
Properties of Functions
Functions possess several key properties:
- Domain:The set of all possible input values.
- Range:The set of all possible output values.
- One-to-One:Each input value corresponds to exactly one output value.
- Onto:Each output value corresponds to at least one input value.
Types of Functions
There are various types of functions, each with its unique characteristics:
- Linear Functions:Functions with a constant rate of change.
- Quadratic Functions:Functions that represent a parabola.
- Polynomial Functions:Functions that are defined by a polynomial equation.
- Exponential Functions:Functions that represent exponential growth or decay.
- Logarithmic Functions:Functions that are the inverse of exponential functions.
Domain and Range
The domain and range of a function are crucial aspects to consider:
- Domain Restrictions:Certain functions may have restrictions on their input values, such as excluding negative numbers or values outside a specific interval.
- Range Restrictions:Some functions may also have restrictions on their output values, such as being positive or bounded within a certain range.
Unit 2 AP Calculus AB Practice: Limits
Limits are a fundamental concept in calculus, providing a means to analyze the behavior of functions as their inputs approach specific values. Understanding limits is crucial for studying derivatives, integrals, and other advanced calculus topics.
Definition of Limits
A limit describes the value a function approaches as its input approaches a particular value. Formally, the limit of a function f(x) as x approaches a (denoted as lim_(x->a) f(x)) is a value L if for any positive number ε, there exists a positive number δ such that if 0< |x - a| < δ, then |f(x) - L| < ε.
Methods for Finding Limits
Various methods exist for finding limits, including:
- Substitution:Direct substitution of the limit value into the function.
- Factoring:Factoring and canceling out common factors in the numerator and denominator.
- Rationalization:Multiplying and dividing by the conjugate to eliminate radicals in the denominator.
- L’Hôpital’s Rule:Used when the limit results in an indeterminate form (0/0 or ∞/∞).
Applications of Limits
Limits have wide-ranging applications in calculus, including:
- Definition of Derivatives:Limits are used to define the derivative of a function as the limit of the difference quotient.
- Definition of Integrals:Limits are used to define the integral of a function as the limit of Riemann sums.
- Analysis of Function Behavior:Limits can determine whether a function is continuous, differentiable, or has vertical or horizontal asymptotes.
Unit 2 AP Calculus AB Practice: Derivatives

Derivatives are a fundamental concept in calculus that measures the rate of change of a function. They provide valuable insights into the behavior of functions and have wide-ranging applications in various fields.
Definition of Derivatives
A derivative is the instantaneous rate of change of a function with respect to its input variable. It represents the slope of the tangent line to the graph of the function at a given point. Mathematically, the derivative of a function f(x) with respect to x is denoted as f'(x) and is defined as the limit of the difference quotient:“`f'(x) = lim (h
- > 0) [f(x + h)
- f(x)] / h
“`
Methods for Finding Derivatives
There are several methods for finding derivatives, including:
-
-*Power Rule
For a power function f(x) = x^n, the derivative is f'(x) = nx^(n-1).
- h(x), the derivative is f'(x) = g'(x)
- h(x) + g(x)
- h'(x).
- h(x)
- g(x)
- h'(x)) / h(x)^2.
- h'(x).
-*Product Rule
For a product of two functions f(x) = g(x)
Unit 2 AP Calc AB practice can be a bit of a challenge, but with a little effort, you can master the material. For a break from the heavy calculus, check out the Twin Peaks drink menu for 2023 . They have some delicious new options that are perfect for sipping on a warm summer day.
Then, come back refreshed and ready to tackle those derivatives!
-*Quotient Rule
For a quotient of two functions f(x) = g(x) / h(x), the derivative is f'(x) = (g'(x)
-*Chain Rule
For a composite function f(x) = g(h(x)), the derivative is f'(x) = g'(h(x))
Applications of Derivatives
Derivatives have numerous applications in calculus, including:
-
-*Optimization
Finding the maximum or minimum values of a function.
-*Related Rates
Solving problems involving rates of change.
-*Curve Sketching
Determining the shape and characteristics of a function’s graph.
-*Applications in Physics
Calculating velocity, acceleration, and other physical quantities.
Unit 2 AP Calculus AB Practice: Applications of Derivatives: Unit 2 Ap Calc Ab Practice
In this unit, we will explore the various applications of derivatives in solving optimization problems and analyzing the behavior of functions. We will delve into real-world examples to illustrate the practical significance of derivatives.
Optimization Problems
Derivatives play a crucial role in optimization problems, where we seek to find the maximum or minimum value of a function. By finding the critical points (where the derivative is zero or undefined) and analyzing the second derivative, we can determine the nature of these extrema.
- Absolute Maximum:The highest point on the graph of a function within a given interval.
- Absolute Minimum:The lowest point on the graph of a function within a given interval.
- Local Maximum:A point on the graph of a function that is higher than all other points in a small neighborhood around it.
- Local Minimum:A point on the graph of a function that is lower than all other points in a small neighborhood around it.
Analyzing Function Behavior, Unit 2 ap calc ab practice
Derivatives also provide valuable insights into the behavior of functions. By studying the sign of the derivative, we can determine whether a function is increasing or decreasing, and by examining the second derivative, we can analyze concavity.
- Increasing Function:A function whose derivative is positive at a given point.
- Decreasing Function:A function whose derivative is negative at a given point.
- Concave Up:A function whose second derivative is positive at a given point.
- Concave Down:A function whose second derivative is negative at a given point.
Real-World Applications
Derivatives have numerous practical applications in various fields, including:
- Economics:Maximizing profit or minimizing cost functions.
- Physics:Determining the velocity and acceleration of an object.
- Engineering:Optimizing the design of structures or machines.
- Medicine:Determining the optimal dosage of medication.
Unit 2 AP Calculus AB Practice: Integrals
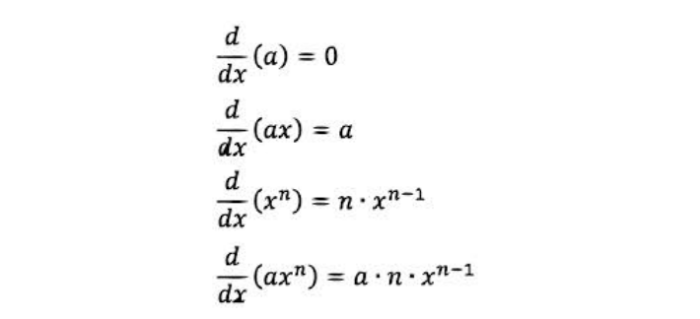
Integrals are a fundamental concept in calculus that allows us to calculate the area under a curve, the volume of a solid, and many other important quantities. In this unit, we will explore the different methods for finding integrals and discuss their applications in calculus.
Methods for Finding Integrals
- The Power Rule:This rule allows us to find the integral of a power function.
- The Sum Rule:This rule allows us to find the integral of a sum of functions.
- The Product Rule:This rule allows us to find the integral of a product of functions.
- The Chain Rule:This rule allows us to find the integral of a composite function.
- Integration by Substitution:This technique allows us to find the integral of a function by substituting a new variable.
- Integration by Parts:This technique allows us to find the integral of a product of two functions.
Applications of Integrals in Calculus
- Calculating the Area Under a Curve:Integrals can be used to find the area under a curve, which is useful for applications such as finding the volume of a solid or the work done by a force.
- Calculating the Volume of a Solid:Integrals can be used to find the volume of a solid, which is useful for applications such as finding the volume of a cone or a sphere.
- Calculating the Work Done by a Force:Integrals can be used to find the work done by a force, which is useful for applications such as finding the work done by a spring or a motor.
Unit 2 AP Calculus AB Practice: Applications of Integrals
In this unit, we will explore the various applications of integrals, focusing on their use in finding volumes and areas. We will also delve into real-world examples where integrals play a crucial role.
Applications of Integrals in Finding Volumes
Integrals provide a powerful tool for calculating the volumes of three-dimensional objects. By integrating the cross-sectional area of an object over its length, we can determine its total volume.
- Method of Slicing:This method involves slicing the object into infinitesimally thin cross-sections and finding the area of each cross-section. The sum of these areas, represented by an integral, gives the volume of the object.
- Method of Shells:This method is used for objects with cylindrical or conical shapes. It involves rotating a thin rectangular strip around an axis to form a shell. The integral of the shell’s volume over the length of the axis gives the total volume of the object.
Applications of Integrals in Finding Areas
Integrals can also be used to find the areas of two-dimensional regions. By integrating the height of a region over its base, we can determine its total area.
- Area Under a Curve:The integral of a function over an interval gives the area under the curve bounded by the x-axis and the function.
- Area Between Curves:When two curves intersect, the integral of the difference between the upper and lower curves over the interval of intersection gives the area between the curves.
Real-World Applications of Integrals
Integrals have numerous applications in various fields:
- Physics:Calculating work, energy, and fluid flow.
- Engineering:Determining the volume of tanks, pipelines, and other structures.
- Economics:Finding the total revenue, cost, or profit over a period of time.
- Biology:Modeling population growth and decay.
FAQ Resource
What is the significance of functions in calculus?
Functions are the foundation of calculus, representing relationships between variables. They allow us to model real-world phenomena and analyze their behavior.
How do limits help us understand calculus concepts?
Limits provide a way to determine the behavior of functions as input values approach specific points. They are crucial for understanding continuity, derivatives, and integrals.
What are the key applications of derivatives?
Derivatives are powerful tools used in optimization problems, analyzing function behavior, and understanding rates of change. They have applications in physics, engineering, and economics.
How are integrals used in real-world scenarios?
Integrals are essential for finding areas, volumes, and other geometric properties. They have applications in fields such as physics, engineering, and statistics.